microPD model combines reaction-diffusion-advection equations (continuous, discrete or hybrid) to model drug, biomarker and metabolites kinetics with regularized Stokeslets methods to model flow of the interstitial fluid, and a discrete model of tumor cells that can either be digitized from a histology sample, idealized or represented by cell nuclei only.
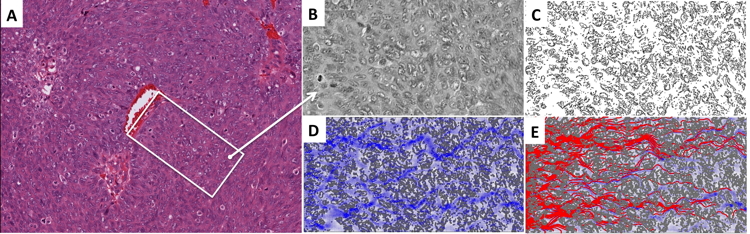
Use fo digitized tumor tissues: (A) an original H&E-stained histological image of ovarian tumor tissue with a centrally located vein. (B) A small patch of tissue selected for digitization (C). (D) The simulated interstitial fluid flow (blue). (E) The resulting traces of the simulated particles representing the drug or biomarker molecules.
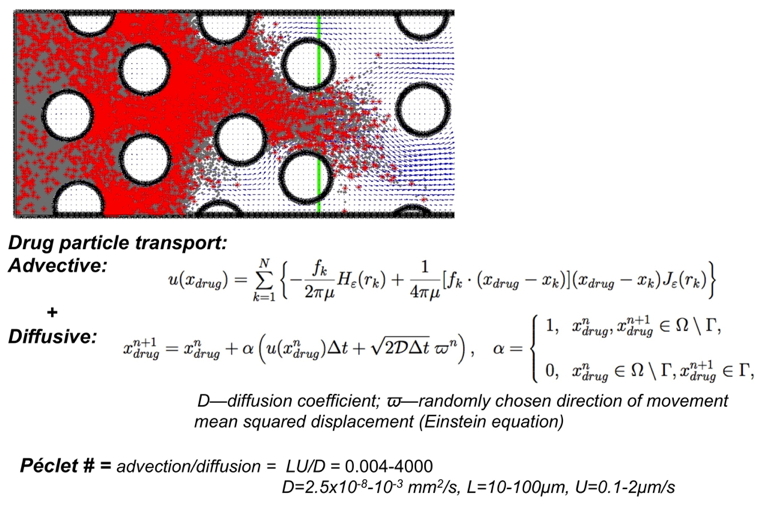
Individual molecules (of the drug or imaging agents under consideration) are modeled as a collection of discrete particles x_drug that enter the tissue via the transmural influx from a capillary (together with the interstitial fluid), and advance through the tissue by a combination of advective transport, with the fluid flow calculated using the regularized Stokeslets method, and diffusion modeled as Brownian motion with a diffusion coefficient D and a randomly chosen direction of movement ϖ. Particle movement (without cellular uptake) is confined to the extracellular space only. The advective transport satisfies this condition since the fluid flow is zero at all cell boundaries. For the diffusive movement we ensure that the particles do not cross the cell membrane incidentally by maintaining their old positions whenever the randomly chosen direction of movement would push the particles into the intracellular space.
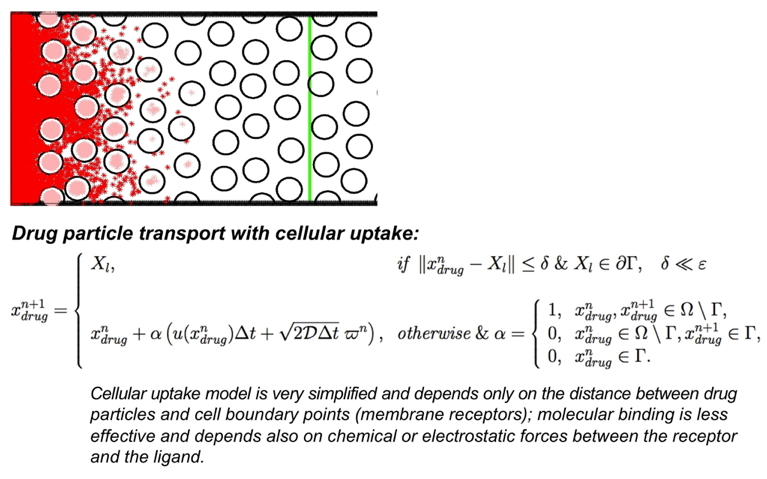
The process of particle internalization by the cells is modeled separately by trapping the particle by the near-by cell boundary receptor if the particle comes close to the cell boundary. This is a very simplified way to model drug uptake, and results in 100% binding rate. However, molecular binding is usually not so efficient, and depends not only on the distance between the receptor and the ligand but also on the chemical or electrostatic forces between the two.
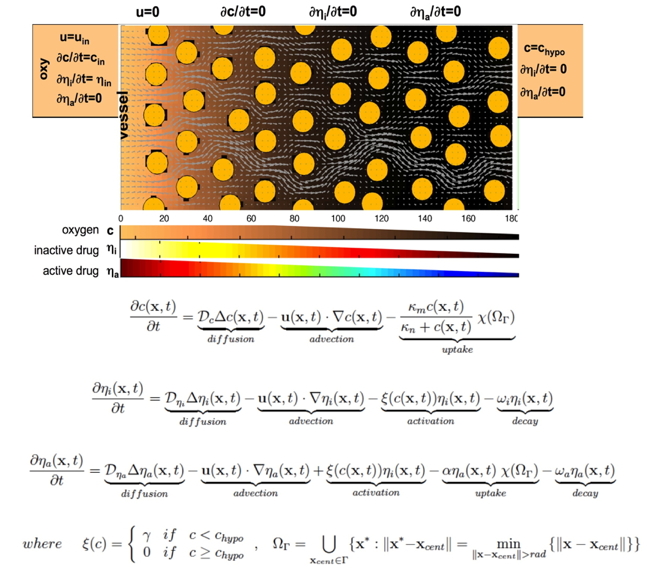
Concentrations of drugs and/or metabolites are modeled using continuous reaction-diffusion-advection eqautions (below) that include terms for decay, activation and uptake. A stable gradient of oxygen through the idealized tissue (with circular cells) is shown below.
![]()