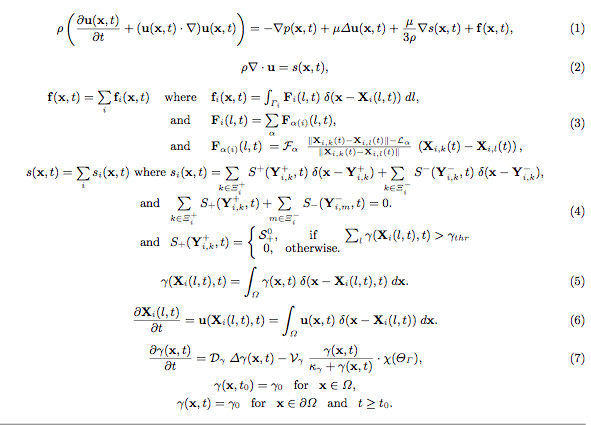Immersed Boundary Method for IBCell:
An immersed boundary framework for modeling the eukaryotic cells
The immersed boundary method captures interactions between immersed elastic bodies (here: cells) and a surrounding incompressible viscous fluid (here: the cytoplasm inside the cells and the extracellular matrix outside the tissue).
Immersed boundary equations of the mechanics of eukaryotic cells:
The model is defined on a two-dimensional domain Ω with fixed Cartesian grid x that is common for the fluid and nutrient variables. The elastic membranes of all cells form a collection Γ of closed curves defined in the curvilinear coordinates X.
The fluid motion is governed by the Navier-Stokes equations (1), where p is the fluid pressure, u is the fluid velocity, the external force density f is defined at the boundaries of all cells Eq.(3), and the source-sink distribution s is taken around all growing cells Eq.(4).
The continuity equation with a source term (2) describes the law of mass balance, where the source distribution s is identically equal to zero on the whole fluid domain except at the point sources and sinks that are used to model cell growth.
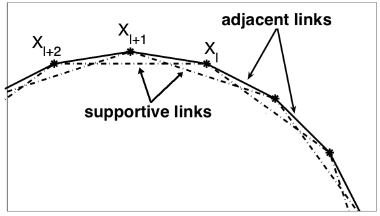
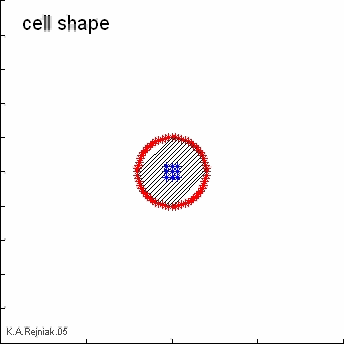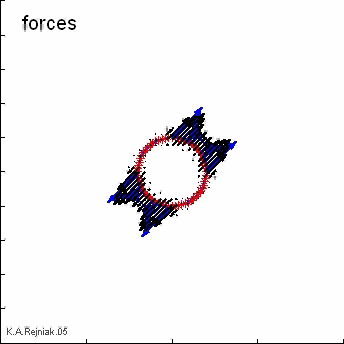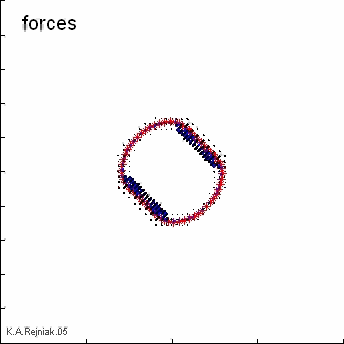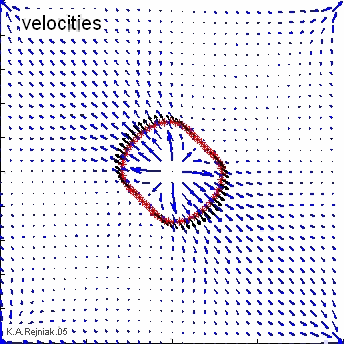
Interactions between the fluid and the material points of all immersed bodies are defined in Eq.(3)-(6). Here, the boundary forces F in the cell X represent the sum of different contractive-repulsive forces arising from elasticity of the cell plasma membrane (adjacent and supportive links), division of the host cell into two daughter cells (along the arrows) and from interactions between distinct cells (adhesive links between boundary points of distinct cells). Each of them satisfies Hooke's law with a constant resting length L and a constant spring stiffness F.
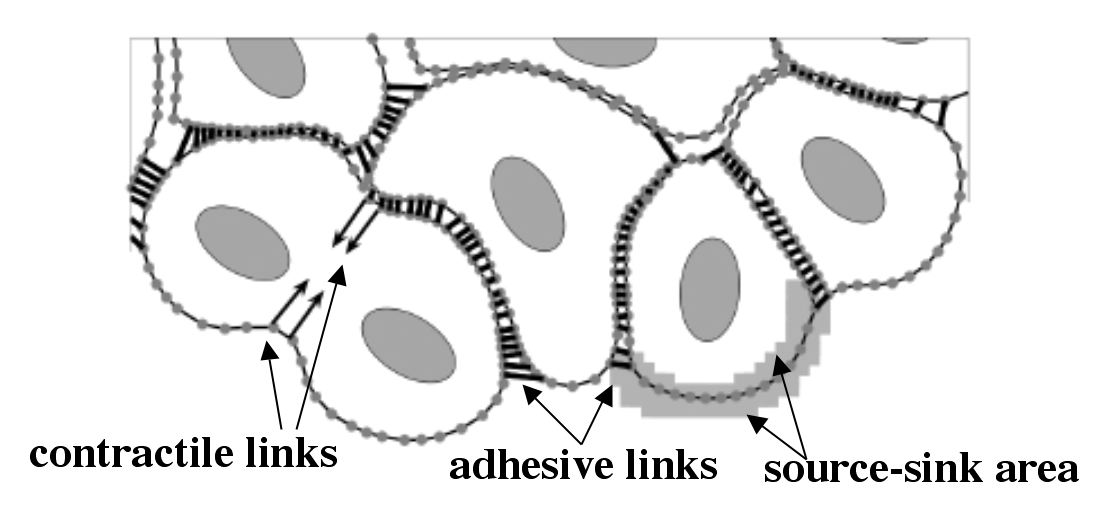
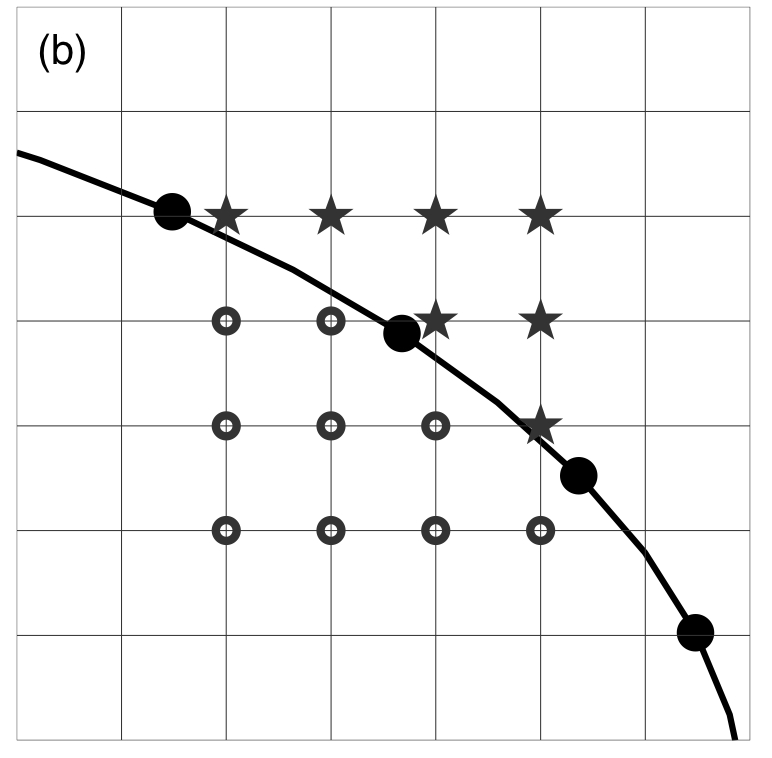
These forces are applied directly to the fluid in a δ -layer region around the boundary Γ Eq.(3) and Figure (a), where δ is a two-dimensional Dirac delta function.
S+ and sinks S- are distributed at the discrete collections Ξ of points Y located along the cell boundary Γ within the cell local micrioenvironment Θ . They are used to model transport of the fluid through the membrane of a growing cell in such a way, that fluid introduced in the sources Y+ inside the cell is balanced by the loss of fluid in the sinks Y- outside the cell membrane for each growing cell separately. These source and sink contributions are then transmitted to the surrounding fluid using the Dirac delta function Eq.(4) and Figure (b).
In this model, the growth and survival of each cell depend on the concentration of nutrients γ in the cell vicinity. Therefore, the activation of fluid sources in the cell takes place when the total concentration of nutrients at all boundary points of that cell exceeds the prescribed threshold value. The value of γ at the material point X is equal to its local concentration around that point Eq.(5). The strength of each balancing fluid sink S- is determined for each host cell separately to balance the total source distribution in that cell Eq.(4).
The no-slip condition of a viscous fluid implies that the material points on cell boundaries are carried along with the fluid Eq.(6).
The kinetics of γ includes a constant source continuously applied at the domain boundaries, uniform diffusion in the whole computational domain and its degradation defined using the Michealis-Menten formulation that takes place within the local microenvironment of all cells. It is also assumed that initially the whole computational domain Ω is filled uniformly with an optimal concentration Eq.(7).
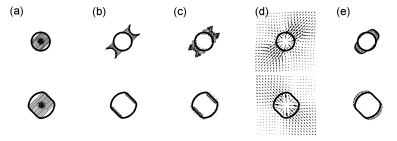
An simulation movie showing the idea behind the immersed boundary method--the interplay between the off-diagonal forces and a central point source in the growing cell. Top row: (a) due to the stretching of the off-diagonal forces (b) that are transmitted to the fluid grid (c), the resulting fluid flow is directed along the force field (d) and the cell growth is off-diagonal (e); Bottom row: the off-diagonal forces are in the resting state (b) and prevent the off-diagonal expansion (c), thus, the fluid flow produced by the active fluid source can only move across the unforced boundaries of the cell (d) and the cell grows along its diagonal (e).
Click for a movie showing the same simulations from three points of view: (1) a growing cell with internal connections and source distribution; (2) boundary (black) and fluid (blue) forces; (3) fluid velocity field (blue) and boundary velocity (black).
More detail on the immersed boundary method of a eukaryotic cell, its numerical implementation and solution can be found in:
• K.A. Rejniak, H.J. Kliman, L.J. Fauci, "A Computational Model of the Mechanics of Growth of the Villous Trophoblast Bilayer", Bulletin of Mathematical Biology, 2004, 66(2):199-232. available on: http://dx.doi.org/10.1016/j.bulm.2003.06.001
• K.A. Rejniak, "An immersed boundary framework for modelling the growth of individual cells: an application to the early tumour development", Journal of Theoretical Biology, 2007, 247:186-204. available on: http://dx.doi.org/10.1016/j.jtbi.2007.02.019
![]()